Nesta entrada, vou explicar como chegar às funções que mais nos surgem no quotidiano, na física, e na matemática.
1 - Função reta
Em matemática, uma reta é uma figura geométrica que estabelece o menor percurso possível entre 2 pontos.
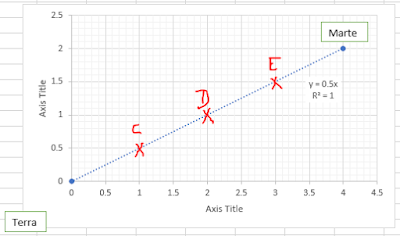
Suponha por exemplo, que lançamos um foguetão a partir da terra, que se encontra nas coordenadas (0,0) e queremos que ele chegue ao planeta Marte, de coordenadas (4,2) gastando o menor combustível possível. Qual função define a trajetória que queremos que o foguetão tome?
R: Como mencionei, a reta é a figura geométrica que se adequa perfeitamente a este exemplo. Ela dá-nos a menor trajetória possível entre 2 pontos. Mas como conseguimos determinar a função que "liga os 2 pontos"?
É bastante simples, a reta tem uma função genérica dada por:
Y = Mx + B
Se soubermos 2 pontos: A ( Xa , Ya) e B ( Xb , Yb) pertencentes à reta, é-nos possível determinar os valores de M e B, com :
E
B = Yb
É a nossa equação da reta
Neste exemplo, o planeta terra encontra-se em A (0,0) e o planeta Marte em B (4 , 2), portanto Ya = 0, Yb =2, Xa = 0, Xb = 4 e indo à nossa expressão genérica obtemos:
Sabendo agora a equação da reta, podemos determinar os pontos C, D e E por exemplo. Sabe-se que:
C: (1, f(1)) = (1, 0.5x1) = (1, 0.5)
D: (2, f(2)) = (2, 0.5x2) = (2, 1 )
E: (3, f(3)) = (3 , 0.5x3) = (3, 1.5)
Se for consultar o gráfico, verá que todos os pontos estão corretos! Detrminámos então matemáticamente o conjunto de todos os pontos que a nave espacial deverá percorrer para que seja gasto o mínimo de combustível possível!
Saber a equação da reta é fundamental na física e na química. Em movimento, por exemplo, o declive da reta em gráficos de velocidade/tempo são a aceleração do objeto, muito presente nas leis de newton. O declive da reta de um gráfico tensão/intensidade de corrente é a Resistência de um aparelho eletrónico. O declive da reta de um gráfico Absorvância /concentração de uma espécie química é o coeficiente de absorção dessa mesma espécie. Entre outros inúmeros exemplos...
2 - Função Parabólica - A parábola / Função afim
A parábola, tal como a reta, é também um exemplo presente na nossa vida sem que nos apercebamos. Matemáticamente falando, a parábola é uma curva plana cujos pontos são equidistantes de um ponto fixo denominado foco, e de uma reta designada diretriz. Coloquialmente falando, a parábola é a curva que uma bola descreve quando é rematada por um jogador de futebol, é a curva das antenas parabólicas, a curva presente nos espelhos da rua para vermos se vem um carro do nosso lado direito, a curva efetuada quando os jogadores de ténis jogam ténis, entre outros inúmeros inúmeros exemplos.
3 - Função racional
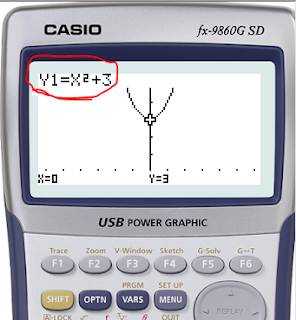
A função racional, tem a expressão geral: Onde k(x) e a(x) são duas quaisqueres funções. A lei de gravitação universal, que nos permitiu determinar a gravidade, o movimento de satélites, planetas, entre outros, é uma função racional. A lei de Coulomb, que nos indica a força elétrica de um circuito por unidade de área, é também uma função racional. Muitos componentes elétricos, tais como Díodos, funcionam segundo uma função racional. Existem inúmeros exemplos para este tipo de funções, sendo por isso fundamental percebê-las. Estas funções tem uma particularidade especial, pois como se sabe, uma vez que resulta de um quociente, a função debaixo nunca poderá ser zero (pois é impossível dividir um número por zero), contudo, é possível estudarmos a função em torno do zero do quociente, que tenderá para infinito! Exemplo : Considere-se a seguinte função: Se formos substituindo x por valores cada vez mais próximos de zero, significa que o resultado da função será cada vez maior. Isto é um típico exemplo de: "Se tentarmos dividir um bolo por um número cada vez menor de pessoas, ficaremos com fatias cada vez maiores, e, teóricamente, se tentarmos dividir um bolo por um número quase 0 de pessoas, essas ficaram com infinitas porções do bolo (que corresponde ao bolo inteiro!). Veja-se a representação gráfica da função: Se x tende para 0, f(x) tende para infinito, negativo ou positivo! Podemos também proceder à translação da função, isto é, fazê-la mover de um lado para o outro. Ao adicionar uma constante, podemos fazer a função subir e descer: Por exemplo: A função abaixo é dada por: Note-se que o x é mentiroso! Isto é, se subtrairmos unidades ao quociente, a função move-se para o lado positivo do eixo x, se adicionarmos, a função move-se para o lado negativo! 4 - Função exponêncial A função exponencial permite descrever o comportamento da evolução da população do Homem, e é bastante utilizada por exemplo em expressões matemáticas de finanças! Esta é dada pela expressão: Exemplo: Ao fazermos aumentar o valor de a, aumentamos o valor da velocidade que a função progride. Veja-se por exemplo: Tal como nas outras funções, podemos fazer a função subir e descer! |













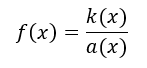


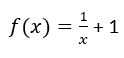






Comentários
Enviar um comentário